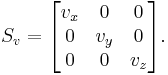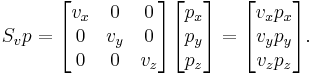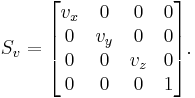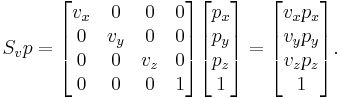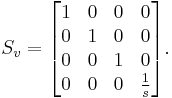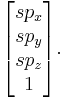Scaling (geometry)
In Euclidean geometry, uniform scaling (isotropic scaling,[1] homogeneous dilation, homothety) is a linear transformation that enlarges (increases) or shrinks (diminishes) objects by a scale factor that is the same in all directions. The result of uniform scaling is similar (in the geometric sense) to the original. A scale factor of 1 is normally allowed, so that congruent shapes are also classed as similar. (Some school text books specifically exclude this possibility, just as some exclude squares from being rectangles or circles from being ellipses.)
More general is scaling with a separate scale factor for each axis direction. Non-uniform scaling (anisotropic scaling, inhomogeneous dilation) is obtained when at least one of the scaling factors is different from the others; a special case is directional scaling or stretching (in one direction). Non-uniform scaling changes the shape of the object; e.g. a square may change into a rectangle, or into a parallelogram if the sides of the square are not parallel to the scaling axes (the angles between lines parallel to the axes are preserved, but not all angles).
Contents |
Matrix representation
A scaling can be represented by a scaling matrix. To scale an object by a vector v = (vx, vy, vz), each point p = (px, py, pz) would need to be multiplied with this scaling matrix:
As shown below, the multiplication will give the expected result:
Such a scaling changes the diameter of an object by a factor between the scale factors, the area by a factor between the smallest and the largest product of two scale factors, and the volume by the product of all three.
The scaling is uniform if and only if the scaling factors are equal (vx = vy = vz). If all except one of the scale factors are equal to 1, we have directional scaling.
In the case where vx = vy = vz = k, the scaling is also called an enlargement or dilation by a factor k, increasing the area by a factor of k2 and the volume by a factor of k3.
A scaling in the most general sense is any affine transformation with a diagonalizable matrix. It includes the case that the three directions of scaling are not perpendicular. It includes also the case that one or more scale factors are equal to zero (projection), and the case of one or more negative scale factors. The latter corresponds to a combination of scaling proper and a kind of reflection: along lines in a particular direction we take the reflection in the point of intersection with a plane that need not be perpendicular; therefore it is more general than ordinary reflection in the plane.
Using homogeneous coordinates
In projective geometry, often used in computer graphics, points are represented using homogeneous coordinates. To scale an object by a vector v = (vx, vy, vz), each homogeneous coordinate vector p = (px, py, pz, 1) would need to be multiplied with this projective transformation matrix:
As shown below, the multiplication will give the expected result:
Since the last component of a homogeneous coordinate can be viewed as the denominator of the other three components, a uniform scaling by a common factor s (uniform scaling) can be accomplished by using this scaling matrix:
For each vector p = (px, py, pz, 1) we would have
which would be homogenized to
Footnotes
- ^ Durand; Cutler. "Transformations" (PowerPoint). Massachusetts Institute of Technology. http://groups.csail.mit.edu/graphics/classes/6.837/F03/lectures/04_transformations.ppt. Retrieved 12 September 2008.
See also
- Scale (ratio)
- Scale (map)
- Scales of scale models
- Scale (disambiguation)
- Scaling in gravity
- Transformation matrix
External links
- Understanding 2D Scaling and Understanding 3D Scaling by Roger Germundsson, The Wolfram Demonstrations Project.